Intervals (lesson)
Contents |
Part 2 – Intervals
In part one of this series we learned about degrees of the scale. We are now ready to take the next step, and talk about intervals. Intervals are the building blocks of chords and harmonies, and we will introduce some language that lets us describe the relationship between any notes, and in the next lesson we will be able to move onto chord construction.
What is an Interval?
An interval is really the distance between 2 notes. Since an interval can’t exist without the note at either end, it is also usually used as a term for the relationship between 2 notes played simultaneously. The numbering for intervals is based on the degrees of the scale, using the major scale we know and love as a template (just as the degrees did in the previous lesson). This will make more sense with an example.
Working in the scale of C (my favourite because it has no sharps or flats) - if we play a C and a G together, what interval is that? Well, the C is the 1st of the scale, and the G is the 5th. To work out the interval, we count the distance between the notes, including the note at each end. So, C,D,E,F,G - 5 notes, which makes the interval a 5th. Ok, what about E and B? Again, look at their degrees. E is the 3rd, B is the 7th. Count the distance - E,F,G,A,B. Its a 5th again!
So we have 2 completely different sets of notes that are a 5th apart, or that make a 5th interval. What actual use is this? Pick up your guitar and play both sets of notes together - play the C and the G together, then play the E and the B together. Although the notes are different, you should be able to hear that they make a similar sound together - this is the characteristic sound of a 5th interval.
Ok, that was fun, lets look at another. Lets try a 3rd this time. Start with a C, and count up 3 degrees - C,D,E. So a C and an E together make a 3rd. What about if we start on a B? You know the drill - B,C,D. B and D together make a 3rd. In this case we went past the end of the scale, and just started again at C. Again, try playing the 2 sets of notes together. You should hear that a 3rd interval sounds quite different in character to a 5th. A 5th sounds harsh and powerful, a 3rd sounds more pleasant and musical.
In the examples above, the 2 different 5ths are enharmonic. That is to say, the intervals are identical. The same is true for the 2 different 3rds.
The Complete Set
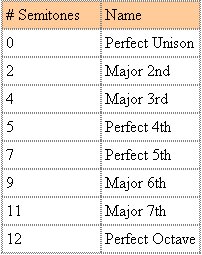
Ok now we know what an interval is, we can list all of them out. At this stage, we are staying within the major scale and looking at notes that occur according to our Major scale formula (T T S T T T S). Different intervals have associated names with them, which I'll list. Bear with me; the names will make sense a little later when we look at interval modifiers.
So what does all of this Perfect and Major business mean? Perfect intervals (Unison, 4th, 5th and Octave) are named because in physical terms the ratio between their frequencies is a simple one. This simple relationship results in a stable sounding tone that is not harsh or dissonant. The remaining intervals are regarded as dissonant, and do not qualify as Perfect intervals for this reason. Dissonance is a little hard to pin down as a concept - it doesn't mean that the intervals necessarily sound bad. 3rds and 6ths are extremely pleasant intervals, 2nds sound awful, this is more of a concept relating back to the physics of the sounds, so don't waste too much energy worrying about it. You can say either 5th or perfect 5th. In common usage the terms are interchangeable.
So much for perfect intervals, what about the Major intervals? Well, that gets a little more interesting ...
Interval Modifiers
If we only had the intervals listed above, we could only ever construct major scales, which is a little limiting. At the top of this lesson I promised you that we would be able to describe relationships between any notes, so now we will look at enhancing this basic framework to enable us to describe intervals in any kind of scale context. Bear in mind that although this framework is based on the major scale, that is just a starting point. These intervals along with the modifiers we are about to learn will work in any scalar context - we are just describing a mechanism to state the distance between any 2 notes in any scale whatsoever, its just convenient to use the major scale as a starting point.
We can modify the relationships between notes in an interval by adding or subtracting semitones from the difference between the 2 notes (or by sharpening or flattening the individual notes, which is the same thing). When we do this, we change the naming convention to reflect this. There are different names for Major and Perfect intervals that are modified in this way.
Looking at Majors first, we can either raise or lower the pitch of one of the notes. Going back to our Major 3rd interval - the notes C and E. We can make that a minor 3rd interval by flattening the E to an Eb. Or, we could make it an augmented 3rd, by raising the sharpening the E to an F (as there is no E#). This particular case is interesting, because if you were paying attention you would have noticed that our augmented 3rd, is exactly the same as a perfect 4th - this is another example of 2 intervals being enharmonic.
When we talk about modifying intervals, its usually best to think in terms of moving the higher note of the two. Moving the lower makes no difference to the constriction of the interval as we are really only interested in the difference between the notes, but when looking at musical function of intervals, the bottom note is often the anchor or reference to what we are trying to do, and moving that will completely change the function of the interval in the context of the music. Looking again at our example 3rd. If we sharpen the C instead of flattening the E, we will still end up with a Minor 3rd interval, C# - E, but the musical context has changed. We are now looking at notes in the scale of C#, not the scale of C. This may very well be what you want to achieve, but until you are confident, stick to altering the higher note of the interval, it will make more sense.
In addition, if you lower the top note of a major interval by 2 steps, it becomes diminished.
So now we know about Diminished, Minor, Major and Augmented intervals. Their relation ship is as follows, adding a semitone to the top note each time:
Diminished -> Minor -> Major -> Augmented
You can do this to any of the major intervals - 2nds, 3rds, 6ths, 7ths. Looking at our 3rd example again, we can count the number of tones for each of these variations as so:
Perfect intervals are similar, but the rules are slightly different. Raise a Perfect interval by a semitone and it becomes augmented. Lower it by a semitone and it becomes diminished. So we have the sequence below, each differing by a semitone:
Diminished -> Perfect -> Augmented.
Taking a 5th interval as an example, we can write the number of tones like this:
An Alternative Terminology
Classical music theory names intervals exactly as described above, however it is common to use a slightly different naming convention in musical discussion, and especially when talking about chord construction.
The difference is in how we specify the major, minor and augmented labels. As we will see in later lessons, due to their importance the 3rd of chords and scales is often still referred to in the way described above, but for other intervals we introduce some new terminology. This terminology is not generally used for the case in which we are describing gaps between arbitary notes, but is used extensively to describe scale degrees and notes in chords.
- A minor interval becomes a 'flat' interval (as it has been moved down one semitone), for instance a 'b5'. Occasionally used for a 3rd, e.g. b3
- An augmented interval becomes a 'sharp' interval (as it has been moved up one semitone), for instance a '#4'
- 7th intervals get special treatment, again because they are important in chord function. A Major 7th keeps its name, a minor 7th can be called either a 'b7' or a 'Dominant 7th'
In addition when putting chords together, it is common to use numbers greater than 7 - this makes sense when you consider how the chords are begin constructed. If we want to add for instance a 2nd to a chord, we will commonly do this using notes higher than the octave note (which is an 8th), so we talk about a 9th interval, which is in reality a 2nd interval moved up an octave - a 2nd is the root note plus one interval, the 9th is an octave (or 8th) pus one. This falls naturally out of the way we stack notes on top of each other to actually build the chords. The rule is that for intervals above 8, just subtract 7 to find out what they are in more familiar terms. Some common ones are:
- A 9th is the same as a 2nd
- An 11th is the same as a 4th
- A 13th is the same as a 6th
This convention can be combined with the previous one, so we could for instance talk about a b13 note within a chord.
Looking at Intervals in Scales
Ok, now we have a way of describing intervals we can start to put this to work in the language we use to describe all sorts of musical constructs - we'll look at scales first as a taster, and then move onto harmonies, triads, and more complex chords in future lessons.
So far we have described scales using our formulae - for instance, T T S T T T S for a major scale. Each letter in the formula represents an interval. When looking at scales, we very commonly analyse the the scale in terms of intervals, counting from the root note. Since the root note is always assumed, we can now describe a major scale as consisting of a Major 2nd, a Major3rd, Perfect 4th, Perfect 5th, Major 6th, Major 7th. That may seem cumbersome, and no one would really ever do that, but it is a very common practice to describe how scales differ from either the Major or Minor scales - that is a lot more useful. So for instance, the Natural Minor scale itself differs form a major scale by having a Minor 3rd, Minor 6th and a Minor 7th - thats a little more useful.
How about modes? Well, for instance, Mixolydian mode is the same as a major scale with a flattened 7th. (If you don't know what modes are don't worry, we'll cover that in a future lesson).
Final Thoughts
It is very common to leave the qualifiers out when talking in intervals for harmonies and chord construction. When we do this, it is understood that we are referring to the variations present in the major scale. That is Major for 2nd, 3rd, 6th and 7th, and Perfect for 4th and 5th. Another terminology you may come across is use of the words flattened or sharpened to describe intervals - this is most common in chord construction. A flattened 5th (b5) for example is commonly used to describe a 5th interval in which the top note has moved down 1 semitone, so it is really a diminished 5th. Similarly, a b3 would be a minor 3rd. We will see this a lot in the lessons on chords.
That's it for today - in the next lesson we will start looking at chord construction with simple triads.
As usual, questions and feedback is welcome!
Editorial note: published 2007-11-12